中学受験の理科～カロリー計算（熱量計算）は基本パターンがあります！

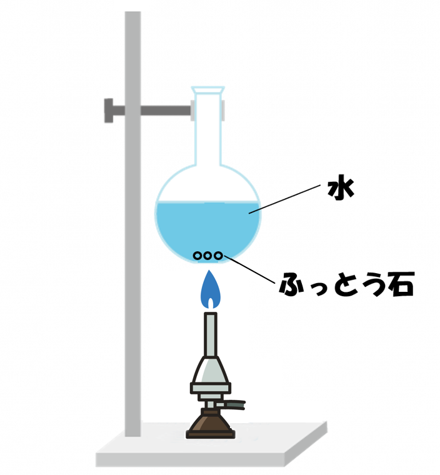
「水」と「熱量（カロリー）」と「温度変化」との関係は、次のようになります。

• 1gの水の温度を1°C上げるのに必要な熱量を、「1カロリー」という。
• 一定量の水に熱をあたえたとき、水の温度変化は、あたえた熱量に比例する。

ルールはとても単純なのですが、いざ問題を解くときに「？」となってしまうことがあります。カロリー計算（熱量計算）をするときには、基本パターンがあることを思い出してくださいね。

本番までに与えられた時間の量は同じなのに、なぜ生徒によって結果が違うのか。それは、時間の使いかたが異なるからです。どうせなら近道で確実に効率よく合格に向かって進んでいきましょう！ くわしくは、以下からどうぞ。
⇒ 中学受験 理科 偏差値アップの勉強法

カロリー計算（熱量計算）の前に・・・

まずは、加えた熱量（カロリー）と、「水の量」「上昇する温度」「熱を加える時間」との関係を整理してみます。

あたためかた（熱の加えかた）が一定の場合、

• 同じ水の量であれば、「上昇する温度」は「熱を加える時間」に正比例する。
• 同じ上昇温度なら、「熱を加える時間」は「水の量」に正比例する。
• 同じ時間であれば、「上昇する温度」は「水の量」に反比例する。

となりますが、考えてしまうと頭が混乱するでしょうから、常識的に考えるほうが良さそうですね。

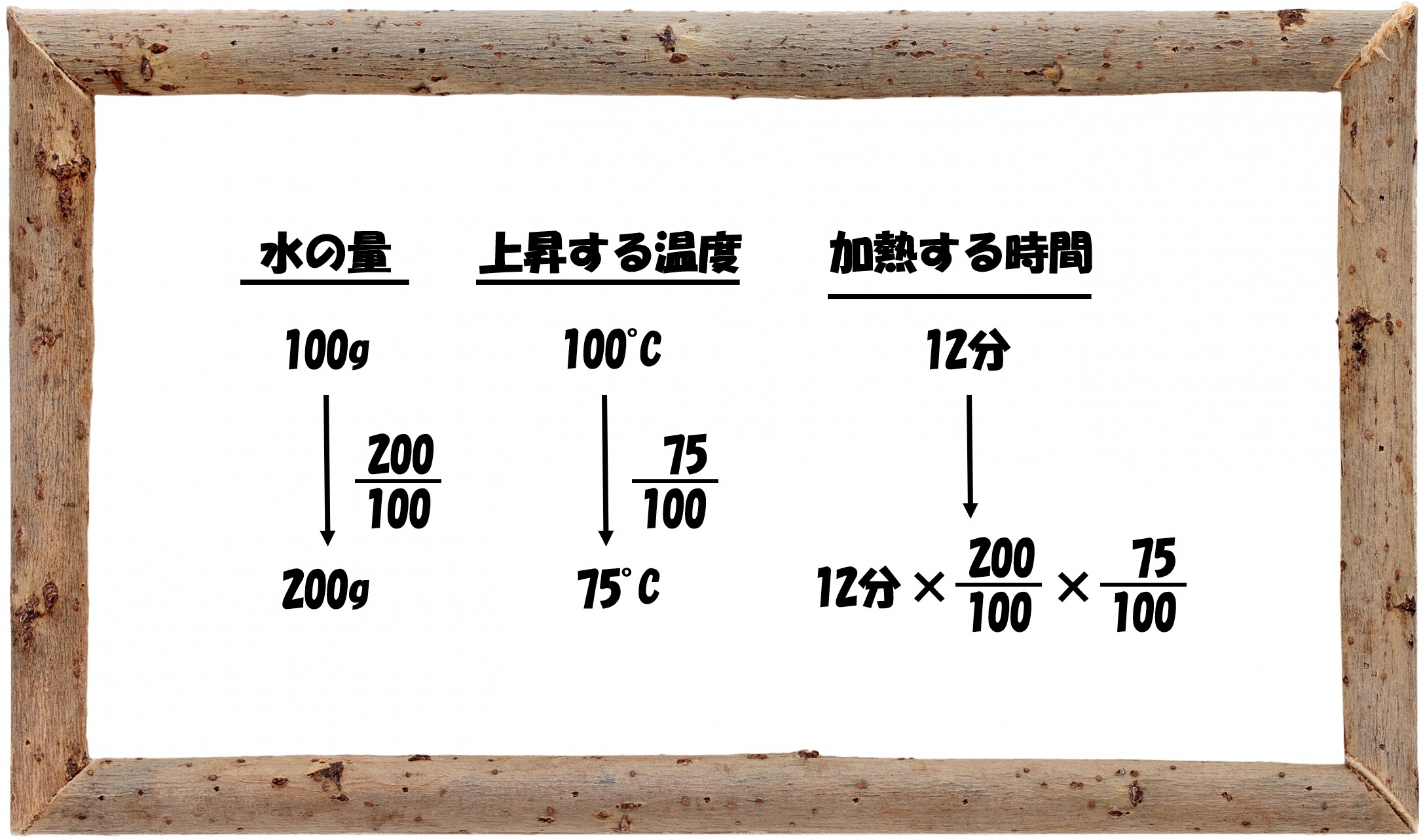
上の問題の場合、「ふっとうするまでの時間」を問われています。つまり、200gの水を75°C（100°C－25°C）だけ上昇する必要があるわけです。

• 「水の量」は2倍だから、時間は長くかかるはず。よって、同じ温度上昇には、2倍の時間がかかるだろう。
• 「上昇する温度」は「100分の75」だから、時間は短いはず。よって、同じ水の量なら、時間は「100分の75」だろう。

つまり、かかる時間は18分（12分×（200 / 100）×（75 / 100））となります。

カロリー計算（熱量計算）のパターン1

量（g）と温度（°C）の異なる水を混ぜる問題には、以下の2パターンがあることになります。

• 水の量（g）が与えられていて、温度（°C）を問われる問題。
• 温度（°C）が与えられていて、水の量（g）を問われる問題。

カロリー計算（熱量計算）のパターン1として、まず「水の量（g）が与えられている」場合を考えます。

解きかたとして、「面積図」や「てんびん図」を使う方法もあるようですが、熱量（カロリー）とは関係ない考えかたなので、オススメしません。「水が持つカロリー（熱量）」をイメージしながら、解くことを心がけましょう。

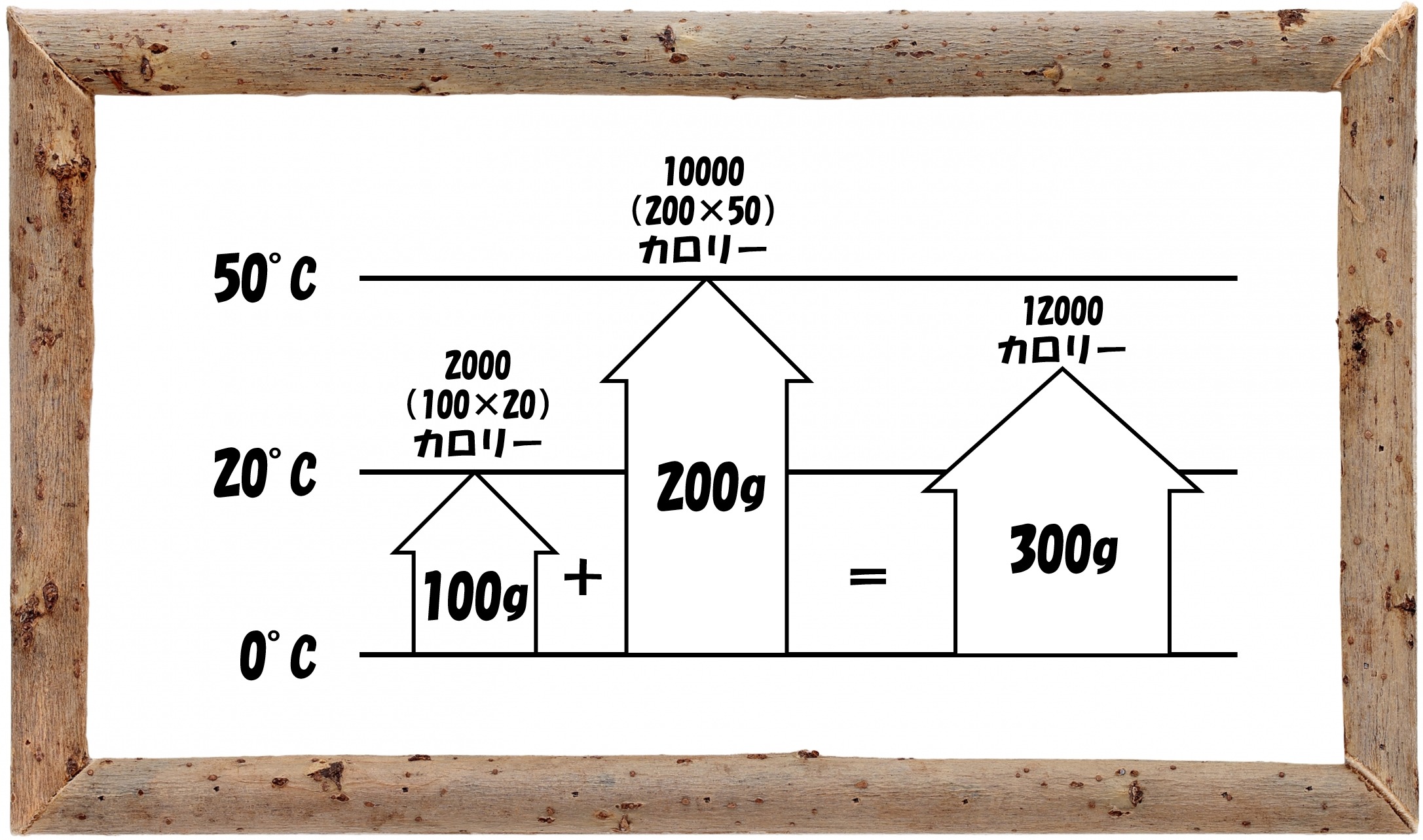
このパターンでは、0°Cを基準（水の温度は0°C～100°C）にして考えると分かりやすいでしょう。土地の高さを、標高（海水面が基準）で考えるのと同じですね。

水の量が与えられていますから、混ぜ合わせた水の量は300g（100g＋200g）。混ぜ合わせた水が持つカロリー（熱量）は、12000カロリー（2000カロリー＋10000カロリー）です。

よって、混ぜ合わせた水の温度は40°C（12000カロリー÷300g）となります。

水の量が与えられる問題として、次のような場合も考えられます。

この場合も水の量が与えられていますから、0°Cを基準にして考えます。

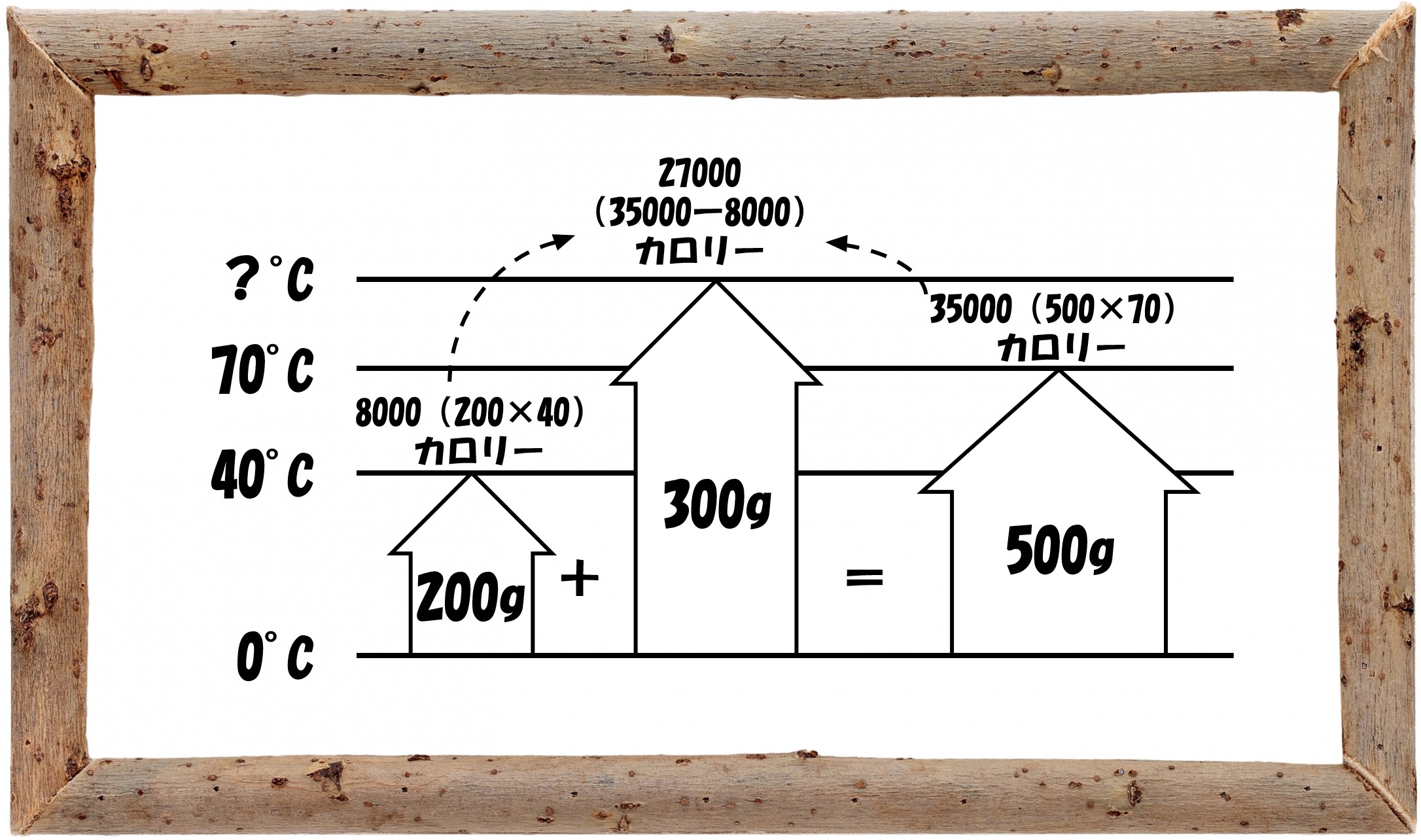
水の量が与えられていますから、混ぜ合わせた水の量は500g（200g＋300g）。混ぜ合わせた水が持つカロリー（熱量）は、35000カロリー（500g×70°C）です。

つまり、300gの水が持っていたカロリー（熱量）は、27000カロリー（35000カロリー－8000カロリー）であったことが分かります。

よって、求める温度は、90°C（27000カロリー÷300g）です。

カロリー計算（熱量計算）のパターン2

カロリー計算（熱量計算）のパターン2は、温度（°C）が与えられていて、水の量（g）を問われる問題です。

この場合は、0°Cを基準にする考え方（下図）では、解きにくくなってしまいます。2つの水について、量・カロリーともに分からないからです。

もちろん、5°Cの水を□gとして、次の式を解くことができれば良いわけですが。

□g×5°C＋100g×85°C＝（□＋100）g×25°C

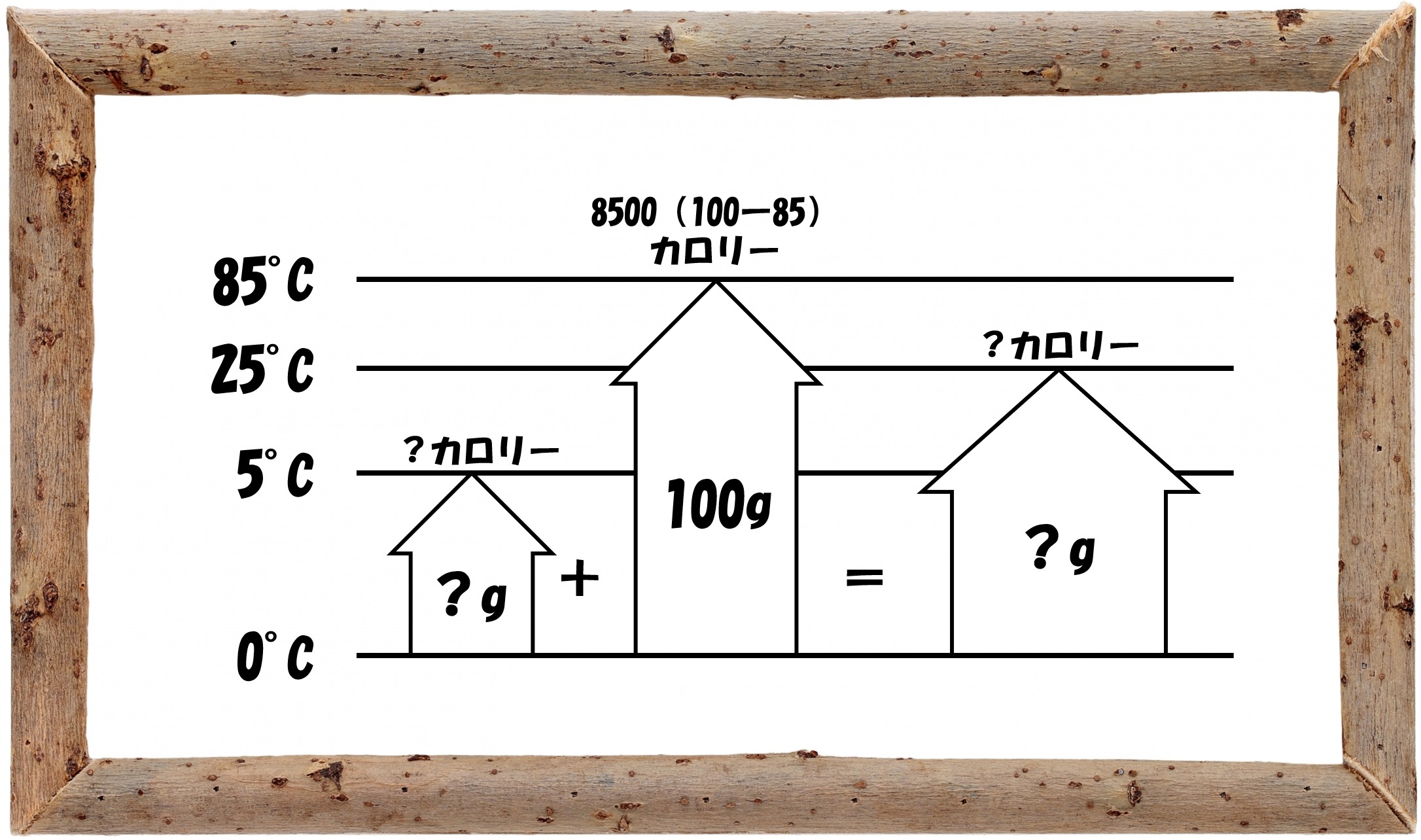
このパターンでは、次のように考えると、楽に解くことができます。

「混ぜる前の水1が得た熱量＝混ぜる前の水2が失った熱量」

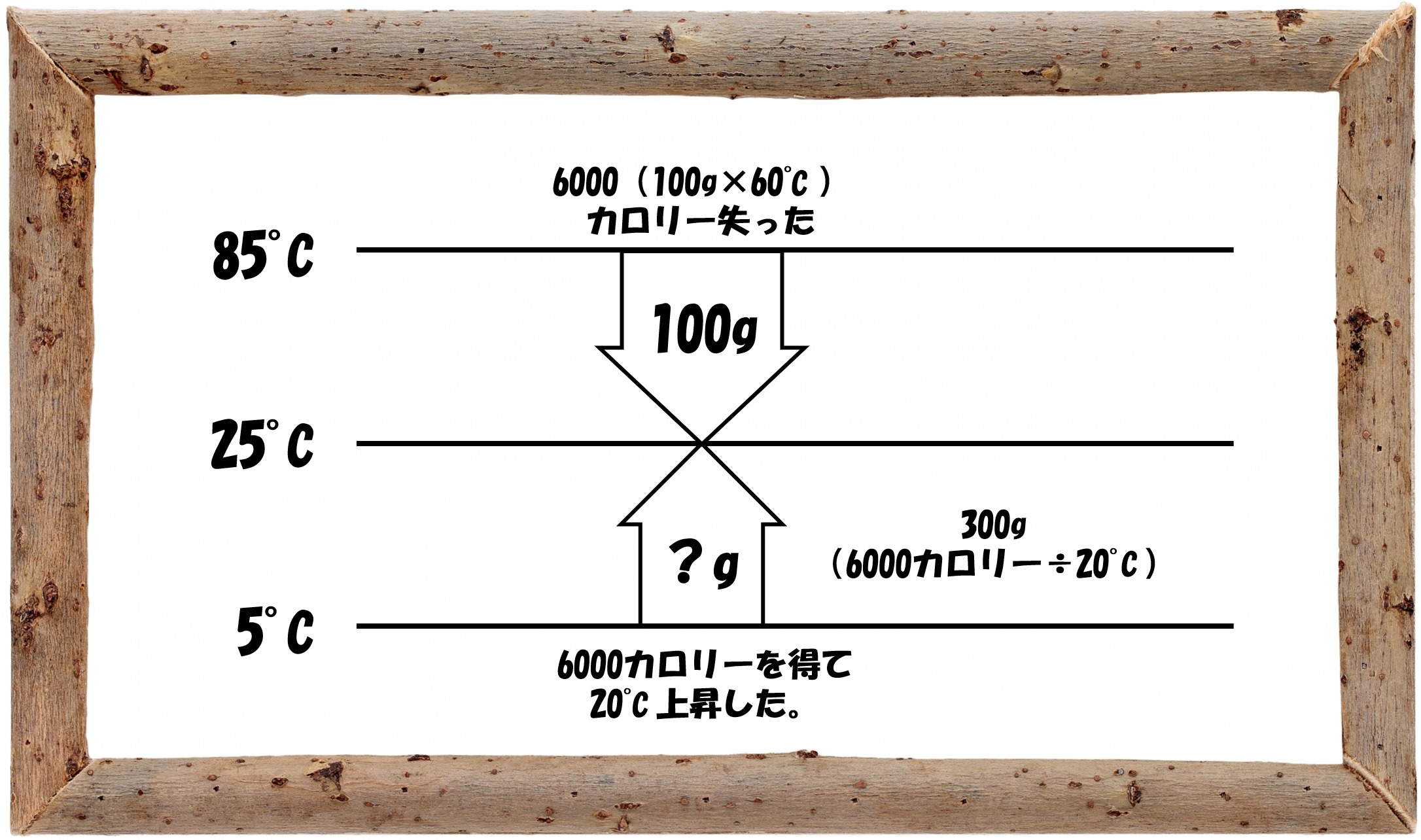
85°Cの水100gは、85°Cから25°Cまで60°C下がったのですから、6000カロリー（100g×60°C）失ったことになります。その分だけ「？g」の水がカロリー（熱量）を得て、20°C（25°C－5°C）上がりました。

6000カロリーを得て20°Cだけ温度が上がる水の量とは、300g（6000カロリー÷20°C）です。

以上のように、パターン2では、見方を変えると複雑な式を解く必要はありませんね。